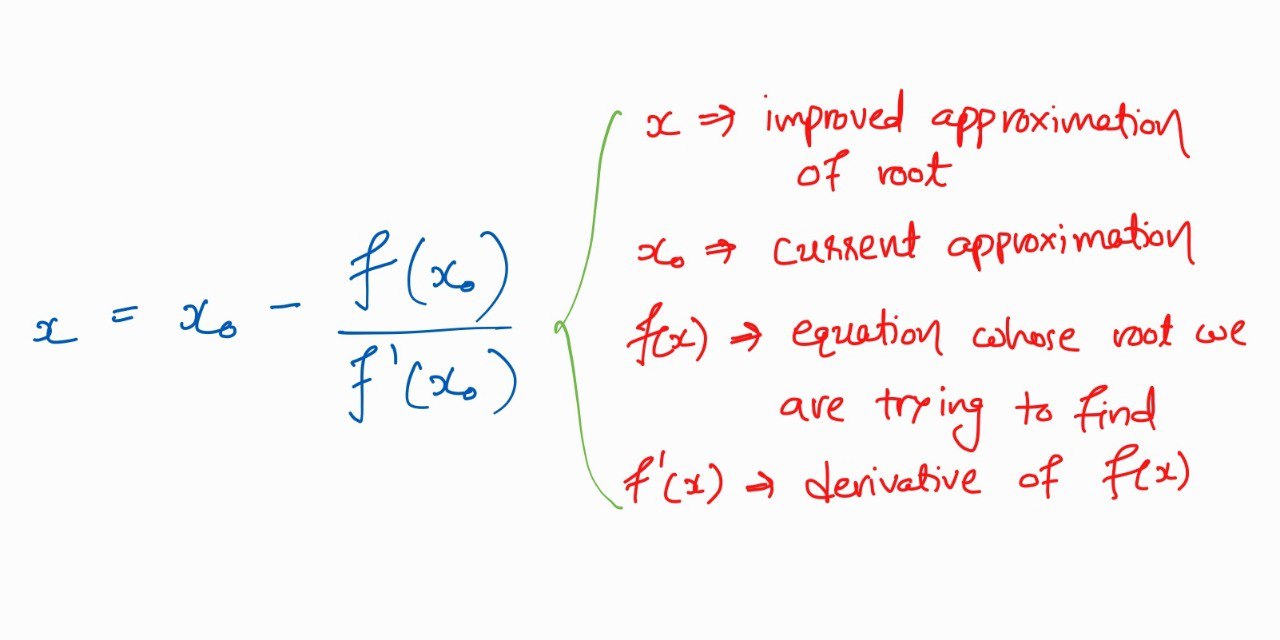
The Newton-Raphson method is a powerful numerical technique for finding the roots of equations.
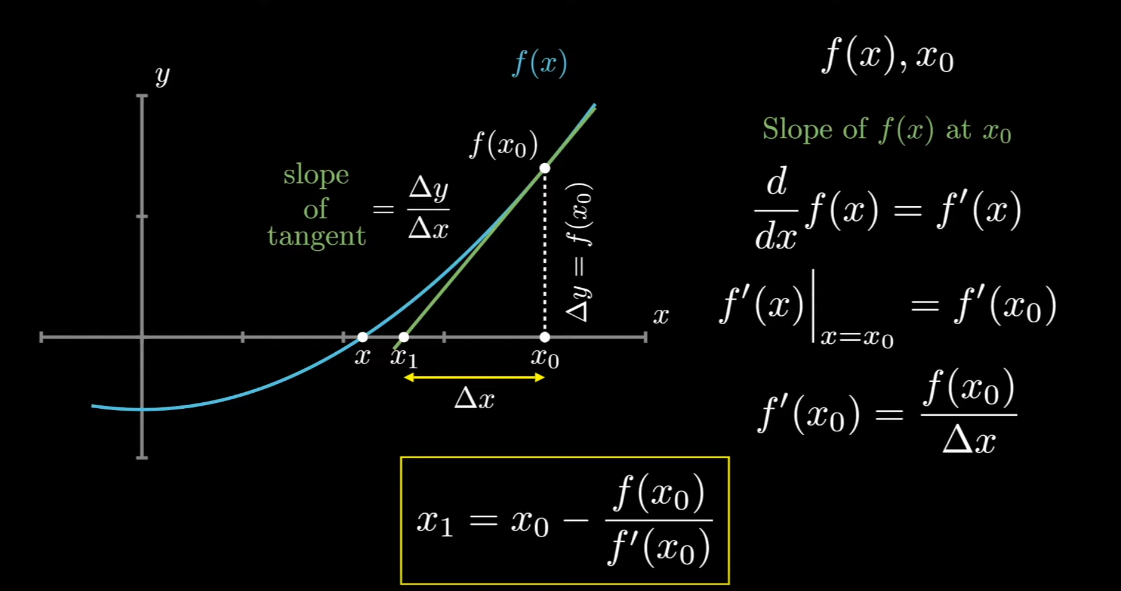
It starts with an initial guess and then improves the guess at each step through an iterative process. To accomplish this, the method uses the equation of the tangent line to the curve defined by the equation at the point of the current guess. The tangent line touches the curve at a single point and has the same slope as the curve at that point.
Mathematical Foundation
The Newton-Raphson method involves iteratively applying a specific formula that converges rapidly to the actual root. For calculating square roots, this method is particularly efficient and accurate.
Algorithm Implementation
To find the square root of a number n without using the built-in sqrt() function, we can reformulate the problem as finding the root of the equation f(x) = x² - n = 0. The Newton-Raphson iteration becomes:
x₁ = (x₀ + n/x₀) / 2
This formula is repeatedly applied until the desired precision is achieved. The method converges quadratically, meaning the number of correct digits roughly doubles with each iteration.
Practical Applications
The Newton-Raphson method for square root calculation has numerous applications in:
- Computer graphics and 3D rendering
- Scientific computing and simulations
- Signal processing algorithms
- Financial calculations and risk modeling
- Embedded systems where efficiency is crucial
Performance Benefits
This implementation offers several advantages over traditional square root functions:
- Fast convergence with minimal iterations
- High precision control
- Independence from built-in math libraries
- Educational value for understanding numerical methods
